Over the years I’ve been gradually chipping away at the problem of graph hashing. For those who are unfamiliar with graph hashing, here is the basic problem: how do you extend hashing algorithms so that they can operate over directed graphs and not just over strings or trees. This problem has proved to be substantially deep. Hashing trees is very simple: simply recursively hash children nodes in order to compute the hash of the parent. This is a variant of Markle tree hashing, and is a well known solution. This process doesn’t easily extend to graphs since they contain cycles.

The first solution proposed in my pre-print released some time ago is to use graph canonization algorithms. The basic idea is to canonize the entire graph, then hash the string representation of the adjacency list. To compute the hash of a specific node, compute the orbit equivalence class and order those classes. Then the hash of a node can be computed as the hash of the graph combined with the index of that node’s orbit. But that isn’t the end of the story!

Things are about to get more complicated. To explore the design space of algorithms, we could contract all the nodes in an orbit into a single node, then hash that graph. But there’s one hiccup - those contracted nodes could lie in the same orbit in the contracted graph! This is not good - in the pre-print I suggested repeatedly contracting until a fixed point is reached, but this always seemed like a hacky solution. Computing the orbits is an expontential time problem, and repeatedly doing this process over and over is a disaster performance wise.

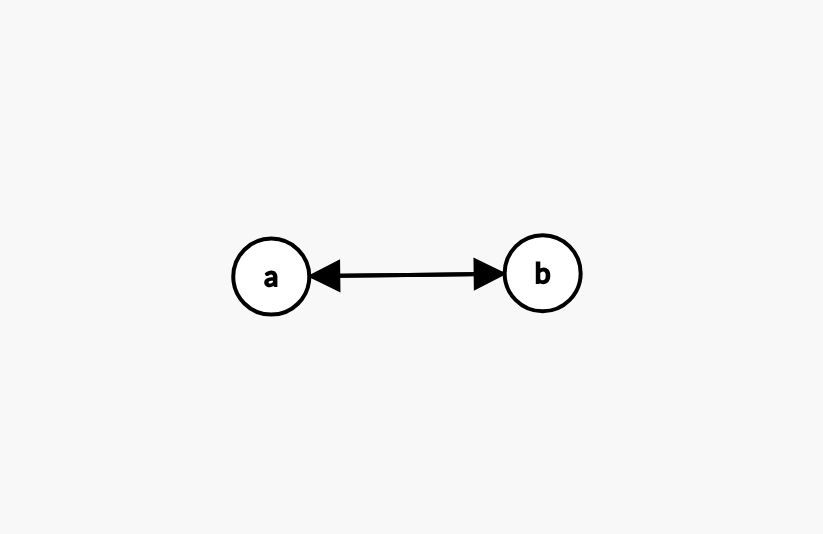The language of the node labeled “a” is {a, ab, aba, abab, …}. The language of the node labeled “b” is {b, ba, bab, baba, …}. The language of the entire graph is the union of the language of all the nodes. In this example the language is {{a, ab, aba, abab, …}, {b, ba, bab, baba, …}}.

Earlier this year I changed the way I approached the problem. In the new approach, the hash of a node in a graph is equivalent to computing the hash of the set of walks one can take from that node. Suppose we have a directed cycle graph with two nodes, one labeled “a” and the other “b”. Then the set of walks for the node labeled “a” is {a, ab, aba, abab, …} and the set of walks for the node labeled “b” is {b, ba, bab, baba, …}. This set-up is very similar to a NFA, but with one twist: instead of accumulating characters by walking along edges, we accumulate characters by visiting nodes. Additionally there is no notion of a “terminal state”. If a node is inside of a cycle, the set of walks is infinite. I call the set of walks the language of a node, and the language of a graph is the set of the languages of all the nodes (a set of set of strings).

If you’ve learned about DFAs before, perhaps you’ve learned about DFA minimization. Here’s the quick summary: for any particular DFA, we can minimize its set of states (nodes) in polynomial time, and furthermore a minimized DFA is unique. Can we do the same thing for our notion of directed graph languages? This would be a great property to have! Initially I thought the answer was no, since NFAs do not have unique minimums. The graph languages have some similarity to NFAs since there is no particular ordering to the edges.

A counterexample that shows that a state-minimum NFA is not unique

There is however a difference between NFAs and these new languages: in NFA minimization the goal is to minimize the number of nodes, but the language is constructed by edges. In our new directed language, the goal is to minimize the number of nodes, but the language is also constructed by nodes. When I translated an analogous version of the above figure into a directed language equivalent, the minimized graphs ended up being isomorphic! After a lot of effort I ended up completing a proof: a minimized directed graph is unique.

The minimization procedure is very much like the one for minimizing DFAs: a table is constructed and initially all nodes are said to be indistinguishable. The first step is to mark all nodes with different labels as distinguishable. Then, just as in the DFA minimization, distinguishability is propagated to parent nodes until the table reaches a fixed point. The primary hiccup in the proof comes from what I call “sublanguages”. If the language of some node is a subset of another, then I call this a sublanguage. If some node s as an edge to another node t, but there is another node t’ where t’ is a sublanguage of t, then it is okay to add an edge from s to t’. I call this process “edge saturation”. This edge saturation post-process step is necessary to get the isomorphism proof to go through.

The proof says that for the language of an entire graph, that language has a unique minimal digraph representation. But I am actually more interested in the language of a node within a graph, not the entire graph. The proof I really want is that if two node languages are equal, then they have a unique minimum digraph. The proof of this is eluding me.

The other thing I’d like to come up with is a polynomial time canonization algorithm for these directed languages. The minimization process guarantees that no two nodes have equal languages. From the minimization algorithm we can find the lexiographically minimum string in the symmetric difference of two node’s languages. We can find the lexiographically minimum string in the difference between the two languages (once again there is a hiccup for sublanguages).

The hope is that these lexiographically minimum strings can act as “markers” that can be used to strictly order the nodes. However once again the proof eludes me, and it’s certainly possible that there’s a counterexample. So perhaps a full blown canonization pass in nauty is still required! While working on this I came up with a dual of edge saturation which I call edge pruning: if some node s has an edge to t and to t’ where t’ is a sublanguage of t, we can remove the edge to t’.

If you have come across this notion of a graph language before, let me know. I’ve been unable to find this particular variation in any research papers. It’s very similar to DFAs/NFAs, so I was a bit suprised to not find anything.

The work in progress proofs and implementations are currently in the lang branch of my dihash repository. See the tex file for the latest proof WIP here: https://github.com/calebh/dihash/blob/lang/papers/lang.tex